２－Ｂ．化学概念（２）

縮重系励起の対称則

遷移金属錯体は、正四面体（T_d）や正八面体（O_h）など高い対称性の構造を有する。そのため、これらの分子軌道には縮重した軌道が現れる。d軌道が分裂してできる3重縮重（t）や2重縮重（e）などがその代表的な例である。遷移金属錯体がさまざまな色をもつのは、このd軌道由来の励起状態が低いエネルギー領域に存在するためである。今日ではTDDFT法やSACCI法などの量子化学計算を行えば、これらの励起エネルギーや遷移強度を容易に求めることができる。計算結果を注意深く調べると、遷移強度がゼロとなる禁制遷移の励起状態も多数含まれることが分かる。さらに、同じ縮重軌道間遷移が主配置である励起状態もいくつか見られる。中井は、この縮重系励起状態には次の規則があることを見出した。さらに、この規則が成り立つ根拠を、凍結軌道解析（FZOA）による解析から説明することに成功した。

縮重系励起の対称則

（１）同じ縮重軌道間遷移が主配置である励起状態のうち、最も励起エネルギーが高い励起状態は許容遷移である（その他の状態はすべて禁制遷移である）

（２）同じ縮重軌道間遷移が主配置である励起状態のうち、許容遷移と禁制遷移の分裂は大きい（禁制遷移間の分裂は小さい）

その後、この規則は遷移金属だけでなく、様々な等核・異核2原子分子（C_∞v, D_∞h）のπ→π*励起（図2-B-1）、ベンゼン（D_6h）のπ→π*励起、B₁₂H₁₂^2-（I_h）の4重縮重したHOMO（g_u）→LUMO（g_g）遷移、C₆₀（I_h）の5重縮重したHOMO（h_u）→3重縮重したLUMO+1（t_g）遷移および5重縮重したHOMO-1（h_g）→3重縮重したLUMO+1（t_u）遷移など、実に多くの場合に成り立つことが確認された。このような汎用性の高さは、分裂の起源が関連する縮重軌道に対する群論と分子積分で説明できるためである（図2-B-2）。そのため、有機分子や無機分子といった分子の個性がほとんど関係しないことは興味深い。

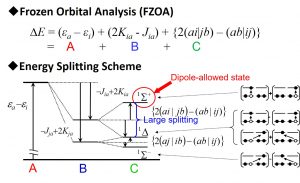
図2-B-1

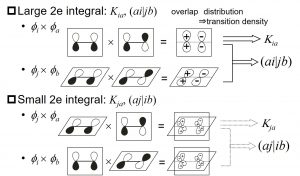
図2-B-2

重要文献

＜FZOA＞

H. Nakai, H. Morita, H. Nakatsuji, “Frozen-orbital analysis for the excited states of metal complexes in high symmetry: O_h case”, J. Phys. Chem., 100, 15753 (1996).
T. Baba, Y. Imamura, M. Okamoto, H. Nakai, “Analysis on excitations of molecules with Ih symmetry: frozen orbital analysis and general rules”, Chem. Lett., 37, 322 (2008).

＜Review＞

H. Nakai, “Rules for excited states of degenerate systems: Interpretation by frozen orbital analysis”, pp. 363-395 in ‘Advances in the Theory of Atomic and Molecular Systems: Conceptual and Computational Advances in Quantum Chemistry’ Progress in Theoretical Chemistry and Physics, P. Piecuch, J. Maruani, G. Delgado-Barrio, S. Wilson (Eds.) (Springer, 2009).

＜日本語解説＞

H. Nakai, “化学原理の発見：縮重系励起の対称則”, J. Comput. Chem. Jpn., 11, 1 (2012).