1-C.実用的な密度汎関数理論: LRD, CVR, ML
LRD | CVR | ML
LRD
今日では、近似的な交換相関汎関数を用いた密度汎関数理論(DFT)計算が普及している。B3LYPなどの従来型の近似汎関数は、無極性分子間にはたらくvan der Waals力の大部分を占める分散力を評価できず、分散力補正が必要となる。中井研究室では、電子密度に依存した第一原理的な分散力補正法として局所応答分散力(LRD)法を開発した。具体的には、原子間および原子対間に働く分散力を電子密度の応答関数からC6, C8, C10,…係数の形で求め、短距離成分を取り除くダンピング関数を用いて、すべての組について足し合わせる。実際、ベンゼンの2量体の計算では、原子間にはC10係数まで、原子対間にはC6係数を用いることで、CCSD(T)計算の結果をよく再現することが示された(図 1-C-1)。
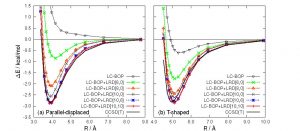
図 1-C-1
LRD法は、電子密度に依存した分散力補正エネルギーを見積ることができるので、閉殻系の基底状態だけでなく、開殻系や励起状態にも適用できる。さらに、Gauss基底を用いる量子化学計算だけでなく、平面波基底を用いる第一原理計算にも用いることができる。LRD法はアイオワ州立大学のMark Gordon研究室で開発されているデファクトスタンダード量子化学計算パッケージGAMESSに実装されており、誰でも利用することが可能である。
重要文献
<LRD>
- T. Sato, H. Nakai, “Density Functional Method Including Weak Interactions: Dispersion Coefficients Based on the Local Response Approximation”, J. Chem. Phys., 131, 224104 (2009).
- T. Sato, H. Nakai, “Local Response Dispersion Method II. Generalized Multicenter Interactions”, J. Chem. Phys., 133, 194101 (2010).
- Y. Ikabata, H. Nakai, “Extension of local response dispersion method to excited state calculation based on time-dependent density functional theory”, J. Chem. Phys., 137, 124106 (2012).
- Y. Ikabata, H. Nakai, “Assessment of local response dispersion method for open-shell systems”, Chem. Phys. Lett., 556, 386-392 (2013).
- Y. Ikabata, Y. Tsukamoto, Y. Imamura, H. Nakai, “Local response dispersion method in periodic systems: Implementation and assessment”, J. Comput. Chem., 36, 303 (2015).
CVR
電子励起状態を計算するための理論として、時間依存密度汎関数理論(TDDFT)がしばしば用いられるが、その計算精度は用いる交換相関汎関数に依存する。価電子励起エネルギーに関しては、B3LYPなどの一般的な汎関数を用いても実験値を比較的よく再現することができるが、電荷移動型の励起状態やRydberg励起状態では、自己相互作用誤差(SIE)を補正できる長距離補正(LC)型の汎関数が必要である。中井研究室では、系統的な数値検証からLDA, GGA, ハイブリッド汎関数いずれを用いても内殻励起エネルギーが過小評価されることを明らかにした。そして、この過小評価を改善するには短距離的なSIEを補正する必要があることを明らかにし、その考察に基づくCore-Valence-Rydberg(CVR)汎関数を提案した。実際、CVR汎関数を用いることでエチレンの内殻励起スペクトルを良好に計算することができた(図 1-C-2)。
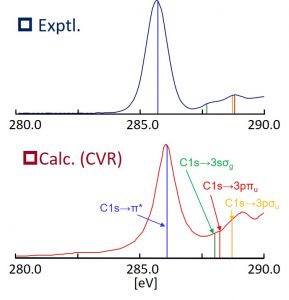
図 1-C-2
重要文献
<CVR>
- A. Nakata, Y. Imamura, and H. Nakai, “Hybrid exchange-correlation functional for core, valence, and Rydberg excitations: Core-valence-Rydberg B3LYP”, J. Chem. Phys., 125, 064109 (2006).
- A. Nakata, Y. Imamura, and H. Nakai, “Extension of the Core-Valence-Rydberg B3LYP Functional to Core-Excited-State Calculations of Third-Row Atoms”, J. Chem. Theory Comput., 3, 1295 (2007).
<Review>
- Y. Imamura, H. Nakai, “Description of core ionized and excited states by density functional theory and time-dependent density functional theory”, pp. 275-308 in ‘Quantum Systems in Chemistry and Physics: Progress in Methods and Applications’ Progress in Theoretical Chemistry and Physics, B 26, K. Nishikawa, J. Maruani, E. J. Brändas, G. Delgado-Barrio, P. Piecuch, (Eds.) (Springer, 2012).
ML
21世紀に入り、ビッグデータへのアクセスが容易になり、それを高速に処理する技術が発展したことにより第3次人工知能(AI)ブームが到来した。その中心的な技術が機械学習(ML)であり、膨大なデータの中に潜む法則を関数として定式化することができる。MLの汎用性は非常に広く、様々な分野で応用されている。中井研究室ではMLを用いて理論化学・計算化学における課題を解決する研究に取り組んでいる。
Kohn-Sham(KS)法のように軌道を導入せずに、電子密度のみの情報からDFT計算を行うには、運動エネルギー汎関数(KEF)の開発が不可欠である。しかし、運動エネルギー項は、交換項や相関項に比べて値が大きいため、それを近似した場合の誤差も必然的に大きくなる。Thomas-Fermi汎関数以降、90年にも及ぶ改良が試みられてきたが、未だに実用的な汎関数には到達していない。中井研究室では、密度や密度勾配などを記述子として、KS法の運動エネルギー密度を目的関数としたML型運動エネルギー汎関数(ML-KEF)を開発した(図 1-C-3)。3次微分まで加えることにより、従来のどの運動エネルギー汎関数より高精度な結果を与えることを確認した(図 1-C-4)。
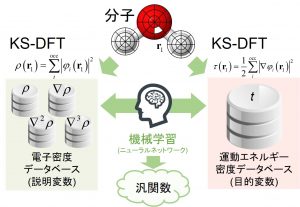
図 1-C-3
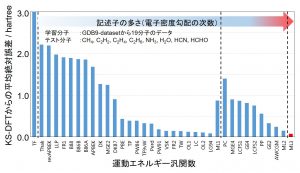 図 1-C-4
図 1-C-4
ML-KEFの成功により、Grid-to-Grid型の機械学習モデルの有効性を確証した。そこで、電子相関エネルギーに対しても同様のアプローチを検討した。記述子には、電子密度、密度勾配、運動エネルギー密度、HF交換エネルギー密度、非整数占有数の電子密度を用いた。Perdew教授が汎関数の階層を表現するために用いたヤコブの縄梯子(Jacob’s Ladder)において、これらの記述子はそれぞれRunge 1, 2, 3, 4, 5に対応する。目的関数は、CCSD(T)/CBS相関エネルギー密度とした。中井研究室では、CCSD(T)/CBS相関エネルギーをMP2/V(DTQ)Z, CCSD/V(DT)Z, CCSD(T)/VDZの相関エネルギーから見積る複合法を提案していた。また、量子化学得計算により得られるエネルギーを空間グリッドごとのエネルギー密度に分割する手法(Grid-EDA)も提案していた。これらの独自技術を用いて、CCSD(T)/CBS相関エネルギー密度を見積った。ML-KEFと同様にニューラルネットワークを用いて、上記の記述子、目的関数から機械学習型電子相関(ML-EC)モデルを構築した。15分子のトレーニングセット、33分子のテストセットを用いたML-ECモデルは、CCSD(T)/CBS相関エネルギーを非常によく再現することが確認された(図 1-C-5)。また、CCSD(T)/CBS相関エネルギーを見積る外挿法や複合法などの従来法に比べて、圧倒的に計算時間が短いことも確認された(図 1-C-6)。
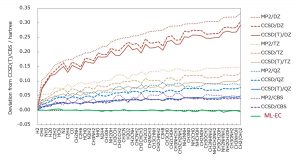
図 1-C-5
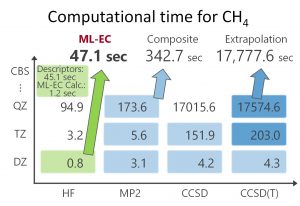
図 1-C-6
重要文献
<ML-KEF>
- J. Seino, R. Kageyama, M. Fujinami, Y. Ikabata, H. Nakai, “Semi-local machine-learned kinetic energy density functional with third-order gradients of electron density”, J. Chem. Phys., 148, 241705 (2018).
<ML-EC>
- T. Nudejima, Y. Ikabata, J. Seino, T. Yoshikawa, H. Nakai, “Machine-learned electron correlation model based on correlation energy density at complete basis set limit”, J. Chem. Phys., 151, 024104 (2019).
- Y. Ikabata, R. Fujisawa, J. Seino, T. Yoshikawa, H. Nakai, “Machine-learned electron correlation model based on frozen core approximation”, J. Chem. Phys., 153, 184108 (2020).
<Composite>
- J. Seino, H. Nakai, “Informatics-Based Energy Fitting Scheme for Correlation Energy at Complete Basis Set Limit”, J. Comput. Chem., 37, 2304 (2016).
