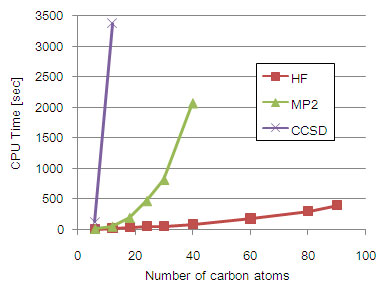
Figure 1. CPU time for HF, MP2, and CCSD calculations of polyenes CnHn+2.
DC法はIowa州立大学のGordonグループで開発されている量子化学計算パッケージGAMESSに実装されています。簡単な使い方はリンクの記事(フリーアクセス)に掲載されています。
DC法に関連した記事が月刊化学に掲載されました。リンクからお読みいただけます。
1. はじめに分子のありとあらゆる物性を司っているのは、電子と原子核の量子論的な振舞いであり、これを明らかにするシミュレーション手段として電子状態計算がある。この振舞いを決定する量子力学の基本方程式(Schrödinger方程式やDirac方程式)はすでに1920年代には確立しており、Paul Dirac (1933年ノーベル物理学賞受賞)は1929年には「化学を数学的に取り扱うための基本法則は完全にわかっている」と述べている。しかし、彼は同時に「原子・分子の一般的な問題に適用すると、厳密には解くことのできない方程式になってしまう」とも述べている。これを近似したモデルを構築し、原子・分子の問題に適用する理論を構築することが、電子状態理論の目的であった。
この近似理論を適用しても、一般に系の大きさが大きくなるほど計算時間が飛躍的に増大して現実的には解くことができなくなってしまう。また、近似の精度を上げる(HF → MP2 → CCSD)ほど計算時間が増大してしまう(Fig. 1)。従って生体分子や固体表面上の化学反応のような実在系の現象を高精度に取り扱うためには、できる限り高いレベルの近似を保ったまま抜本的に計算コストを落とす手法が必要不可欠となる。我々はそれを実現する手法の一つとして、分割統治(Divide-and-Conquer; DC)法の開発を行ってきた。

Figure 1. CPU time for HF, MP2, and CCSD calculations of polyenes CnHn+2.
近代哲学の父、ルネ・デカルトはその著書『方法序説』で次のように述べている。「検討する困難を問題をよりよく解くために必要な小部分に分割せよ」[1]。つまり、大きな系を計算する困難を、より小さな系をいくつも解く計算に分割して解決すればよいのである。Weitao Yangはこのような考え方を電子状態計算に初めて持ち込み、DC法を提案した[2,3]。
まず、Yangが提案した一体近似に基づくDC法の計算手順を説明する(Fig. 2)。全系をまず重なりのない部分系(subsystem)に分割する。この部分系を単にぶつ切りにはせず、部分系の周囲にバッファ領域(buffer region)と呼ばれる緩衝領域を付け加える。バッファ領域を含めた局在化領域(localization region)の中でHartree-Fock (HF)方程式やKohn-Sham (KS)方程式を解き、部分系の分子軌道を得る。この際に、さらに外側の電子や原子核が作る静電場も考慮する。各部分系の情報を平均化して、全系の電子数を保存するように系全体のフェルミ準位を決め、密度行列とエネルギーを求める。この密度から場を作りなおして再計算するという流れを、密度行列とエネルギーが収束するまで繰り返す。DC法で求められるものをまとめると、部分系の分子軌道と全系の密度行列、SCFエネルギーである。
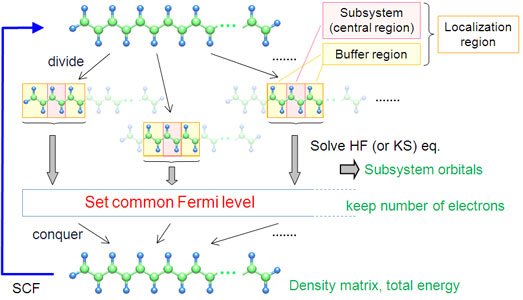
Figure 2. Schematic of the DC SCF procedure.
我々はDC-HF法のアセスメントを系統的に行い、計算時間が大幅に短縮されること、部分系を原子1個にする極限的な場合でも数kcal/mol以下の精度でエネルギーを求めることができることを実証してきた[4,5]。また、DC法は繰り返し計算の収束性が悪いことが知られていたが、これを解決する手法としてDC-DIIS法[4]とDC-FON法[6]を提案してきた。しかし、この手続きではHF法やDFTなどの一体近似的な取り扱いしかできない。我々はさらに、この手法である意味副次的に得られる部分系の分子軌道を用いて、高精度電子状態計算に不可欠な電子相関を取り込む手法を開発した。
一般に電子相関の計算には分子軌道が必要である。DC法で得られる部分系の分子軌道でも電子相関を計算することは可能である。しかし、部分系の分子軌道はバッファ領域にまでまたがっているため、全系の相関エネルギーを求めるために足し合わせてしまうと、余分な足し合わせが生じてしまう(Fig. 3)。そこで、我々の研究室で開発を進めているエネルギー密度解析(EDA)[7]の考え方を利用して、相関エネルギーのうち中央領域だけからの寄与を求め、これを足し合わせる手法を開発した。
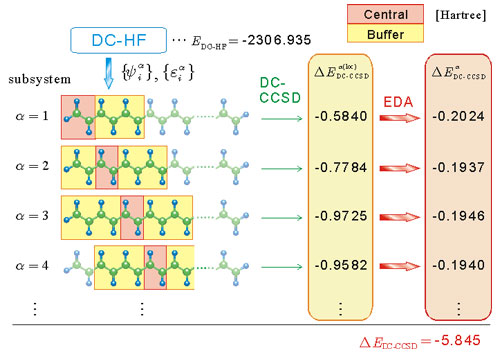
Figure 3. Schematic of the DC-CCSD procedure of polyene C60H62.
我々はこれまでにこの手法をMP2法[8,9]、CCSD法[10]、CCSD(T)法[11]に適用し、その有用性を示してきた。一例として、CCSD法に適用したときの計算時間を示す(Fig. 4)。従来のCCSD法(黒線)では、原子の数に対して6乗のオーダーで計算コストが増大していたものが、DC法を適用した場合(赤線)はほぼ線形まで落とせており、飛躍的に計算時間を短縮することに成功した。
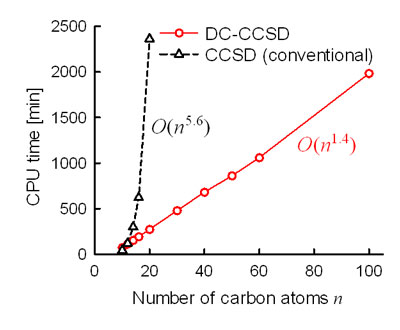
Figure 4. CPU time for DC and conventional CCSD calculations of polyenes CnHn+2.
さらに、この計算で得られたエネルギーの比較を示した(Table 1)。この系では、従来法とDC法の差はほぼ0.1 mhartree以下に抑えられており、高精度な計算が行えていることが確認できる。この計算の誤差は系や用いる基底関数によっても異なるが、バッファの大きさを変えることにより系統的に改善を行うことができる。
Table 1. Comparison of DC and conventional CCSD energies [hartree] of polyenes CnHn+2 (6-31G).
| n | conventional CCSD | DC-CCSD | (diff.) |
|
10 12 14 16 20 |
-386.428 612 -463.483 300 -540.537 753 -617.592 242 -771.699 816 |
-386.428 501 -463.483 218 -540.537 695 -617.592 176 -771.699 772 |
(+0.000 111) (+0.000 082) (+0.000 058) (+0.000 066) (+0.000 045) |
我々は分割統治(DC)法を用いることにより、電子相関を含む高精度な大規模系電子状態計算のコストの削減に成功した。本稿では示さなかったが、MP2計算に対してはDC-HF密度行列の汎関数[12]として相関エネルギーを求めることで計算コストを削減するDC-DM MP2法も提案している[13]。このような計算コスト削減の取り組みは、計算時間を短縮することのみではなく、不可能であったものを可能にしたという重要な意味を持っていることを忘れてはならない。
電子状態計算の発展には、このような理論・アルゴリズムの発展だけでなく、コンピュータの進歩が不可欠である。コンピュータ・アーキテクチャが新しい理論やアルゴリズムを要求することもしばしばある。最近では計算の並列化が高速計算の鍵であるが、DC法は部分系ごとに問題が分割されているので、このようなコンピュータでの利用に非常に向いている。高精度な電子相関理論、高速な並列コンピュータ、そしてDC法の3つがタッグを組むことで、理論化学の新たなパラダイムが開けると確信している。