2-C. Chemical Principle (III)
Controlling Factor of Conical Intersection Structure
In chemistry, stationary points on the potential energy surface (PES) and intersections between multiple PESs are important. Minima on PES correspond to the stable structure of the molecule and determine various properties of the molecule. The first-order saddle points on the PES correspond to the transition states and govern the rates of the chemical reactions. Intersections, that is, conical intersections and intersystem crossings, affect the photophysical properties and photochemical reactions of molecules. The stable structures and transition states of the molecule can be understood by the chemical bond theory based on the electronic state theory, but it was unclear what governs the structures of the conical intersections and the intersystem crossings. In fact, the structures of the minimum energy conical intersections between the singlet ground (S0) and the lowest excited (S1) states (S0/S1 MECIs) is remarkably different from the stable structures in the S0 and S1 states (Fig. 2-C-1).
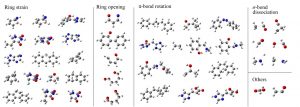
Fig. 2-C-1
By adopting the frozen orbital analysis (FZOA), Nakai’s Group revealed that the exchange integration between HOMO and LUMO is closer to zero in S0/S1 MECI (Fig. 2-C-2). When the overlap of orbitals becomes small, the exchange integration approaches zero generally. Thus, the HOMO and LUMO in the S0/S1 MECI tend not to overlap spatially. Ring strain, ring opening, π bond rotation, and σ dissociation satisfy this requirement.
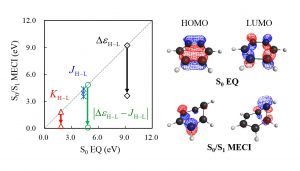
Fig. 2-C-2
Key Literature
<MECI>
- H. Nakai, M. Inamori, Y. Ikabata, Q. Wang, “Unveiling Controlling Factors of the S0/S1 Minimum Energy Conical Intersection: A Theoretical Study”, J. Phys. Chem. A, 122, 8905 (2018).
- M. Inamori, Y. Ikabata, T. Yoshikawa, H. Nakai, “Unveiling controlling factors of the S0/S1 minimum energy conical intersection (2): Application to penalty function method”, J. Chem. Phys., 152, 144108 (2020).
<Review (in Japanese)>
- 稲森 真由, 五十幡 康弘, 王 祺,中井 浩巳, “ポテンシャルエネルギー曲面の交差構造に関する理論的研究”, Comput. Chem. Jpn., 17, 124 (2018).
