2-B. Chemical Principle (II)

Symmetry Rules for Degenerate Excitations

Transition metal complexes have highly symmetric structures such as tetrahedron (T_d) and octahedron (O_h). Therefore, degenerate orbitals appear in these molecular orbitals. Typical examples are triply degenerate (t) and doubly degenerate (e) orbitals formed by splitting the d orbitals. The transition metal complexes have various colors because the excited state related with the d orbitals exists in the low energy region. Nowadays, these excitation energies and transition intensities can be easily demonstrated by performing quantum chemistry calculations such as the TDDFT and SACCI methods. Careful examination of the calculation results reveals that there are many excited states of the forbidden transition in which the transition intensity is zero. In addition, some excited states correspond to the same transitions between the degenerate orbitals. Nakai found that the degenerate system excited states have the following rules. Furthermore, the frozen orbital analysis (FZOA) succeeded in explaining the origin for the rules.

 

Symmetry Rules for Degenerate Excitations

Among the excited states with the same transitions between degenerate orbitals,

（１）the excited state with the highest excitation energy is the dipole allowed transition (all other states are forbidden transitions).

（２）the splitting between the allowed- and forbidden-transition states is large (the splitting between the forbidden-transition states is small).

 

The rules are established not only to transition metal complexes, but also to π → π* excitations of various homo-nucelar and hetero-nucelar diatomic molecules (C_∞v, D_∞h) (Fig. 2-B-1), π → π* excitations of benzene (D_6h), transitions between quadruply degenerate HOMO (g_u) → LUMO (g_g) of B₁₂H₁₂^2- (I_h), transitions between quintuply degenerate HOMO (h_u) → triply degenerate LUMO+1 (t_g) and between quintuply degenerate HOMO-1 (h_g) → triply degenerate LUMO (t_u) of C₆₀ (I_h). The symmetry rules for degenerate orbitals have high versatility, because the origin of splitting can be explained by group theory and molecular integration for degenerate orbitals (Fig. 2-B-2). It is interesting that the molecular characters such as organic molecules and inorganic molecules has less important.

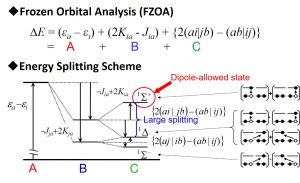
Fig. 2-B-1

 

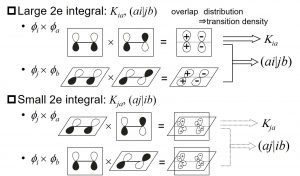
Fig. 2-B-2

 

 

Key Literature

＜FZOA＞

• H. Nakai, H. Morita, H. Nakatsuji, “Frozen-orbital analysis for the excited states of metal complexes in high symmetry: O_h case”, J. Phys. Chem., 100, 15753 (1996).
• T. Baba, Y. Imamura, M. Okamoto, H. Nakai, “Analysis on excitations of molecules with Ih symmetry: frozen orbital analysis and general rules”, Chem. Lett., 37, 322 (2008).

＜Review＞

• H. Nakai, “Rules for excited states of degenerate systems: Interpretation by frozen orbital analysis”, pp. 363-395 in ‘Advances in the Theory of Atomic and Molecular Systems: Conceptual and Computational Advances in Quantum Chemistry’ Progress in Theoretical Chemistry and Physics, P. Piecuch, J. Maruani, G. Delgado-Barrio, S. Wilson (Eds.) (Springer, 2009).

＜Review (in Japanese)＞

• H. Nakai, “化学原理の発見：縮重系励起の対称則”, J. Comput. Chem. Jpn., 11, 1 (2012).