1-C. Practical density functional theory
LRD | CVR | ML
LRD
Nowadays, density functional theory (DFT) calculations using approximate exchange-correlation functionals are widespread. Conventional approximate functionals such as B3LYP cannot evaluate the dispersion force that accounts for most of van der Waals force between non-polar molecules, and requires dispersion correction. Nakai’s Group has developed the local response dispersion (LRD) method as a first-principles dispersion correction method that depends on electron density. The dispersion forces acting between atoms and between atomic pairs are obtained from the response function of electron density in the form of C6-, C8-, and C10-coefficients, and are summed up for all combinations with a damping function that removes short-range components. In the case of the benzene-dimer calculation, the CCSD (T) result is well reproduced by using LRD method with C6-, C8-, and C10-coefficients between atoms and the C6-coefficient between atomic pairs (Fig. 1-C-1).
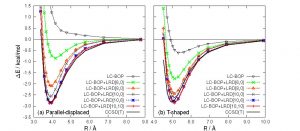
Fig. 1-C-1
Since the LRD method can estimate the dispersion correction depending on the electron density, it can be applied not only to the ground state of the closed shell system but also to the open-shell system and the excited state. Furthermore, it can be used not only for quantum chemistry calculations using Gaussian basis, but also for first-principles calculation using plane wave basis. The LRD method is implemented in the de facto standard quantum chemistry calculation package GAMESS developed at Prof. Mark Gordon’s Group at Iowa State University.
Key Literature
<LRD>
- T. Sato, H. Nakai, “Density Functional Method Including Weak Interactions: Dispersion Coefficients Based on the Local Response Approximation”, J. Chem. Phys., 131, 224104 (2009).
- T. Sato, H. Nakai, “Local Response Dispersion Method II. Generalized Multicenter Interactions”, J. Chem. Phys., 133, 194101 (2010).
- Y. Ikabata, H. Nakai, “Extension of local response dispersion method to excited state calculation based on time-dependent density functional theory”, J. Chem. Phys., 137, 124106 (2012).
- Y. Ikabata, H. Nakai, “Assessment of local response dispersion method for open-shell systems”, Chem. Phys. Lett., 556, 386-392 (2013).
- Y. Ikabata, Y. Tsukamoto, Y. Imamura, H. Nakai, “Local response dispersion method in periodic systems: Implementation and assessment”, J. Comput. Chem., 36, 303 (2015).
CVR
Time-dependent density functional theory (TDDFT) is commonly used as a theory for calculating electronic excited states, but its accuracy depends on the exchange correlation functional used. For valence excitation energies, experimental values can be reproduced relatively well using general functionals such as B3LYP, but in charged-transfer and Rydberg excited states, long-range correction (LC) type functionals to correct the self-interaction errors (SIE) is needed. Nakai’s Group has clarified that the core excitation energy is significantly underestimated by using LDA, GGA, and hybrid functionals from systematic numerical assessment. We clarified that this underestimation is improved by correcting short-range SIE, and proposed a Core-Valence-Rydberg (CVR) functional based on the consideration. By using the CVR functional, the core excitation spectrum of ethylene could be demonstrated well (Fig. 1-C-2).
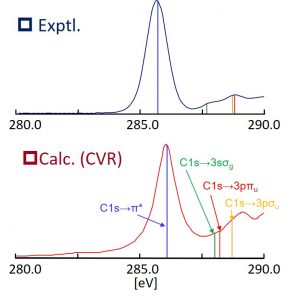
Fig. 1-C-2
Key Literature
<CVR>
- A. Nakata, Y. Imamura, and H. Nakai, “Hybrid exchange-correlation functional for core, valence, and Rydberg excitations: Core-valence-Rydberg B3LYP”, J. Chem. Phys., 125, 064109 (2006).
- A. Nakata, Y. Imamura, and H. Nakai, “Extension of the Core-Valence-Rydberg B3LYP Functional to Core-Excited-State Calculations of Third-Row Atoms”, J. Chem. Theory Comput., 3, 1295 (2007).
<Review>
- Y. Imamura, H. Nakai, “Description of core ionized and excited states by density functional theory and time-dependent density functional theory”, pp. 275-308 in ‘Quantum Systems in Chemistry and Physics: Progress in Methods and Applications’ Progress in Theoretical Chemistry and Physics, B 26, K. Nishikawa, J. Maruani, E. J. Brändas, G. Delgado-Barrio, P. Piecuch, (Eds.) (Springer, 2012).
ML
In the 21st century, the third artificial intelligence (AI) boom has arrived due to the easy access to big data and the development of technology for processing it at high speed. The central technology is machine learning (ML), which can formulate the law hidden in a huge amount of data as a function. The versatility of ML is very wide and it is applied in various fields. Nakai’s Group is working on research to solve problems in theoretical and computational chemistry using ML.
The development of a kinetic energy functional (KEF) is indispensable for performing DFT calculation from only electronic density without introducing an orbit as in the Kohn-Sham (KS) method. However, since the kinetic energy term has a larger value than the exchange and correlation terms, the error when approximating it is inevitably large. Despite that 90 years of improvements have been attempted since Thomas-Fermi functional, no practical functional has been reached so far. Nakai’s Group developed a ML-type kinetic energy functional (ML-KEF) by using the kinetic energy density of the KS method as the objective function as well as the density and density gradient as descriptors (Fig. 1-C-3). By using up to the third derivative, the ML-KEF result is more accurate than any conventional kinetic energy functional (Fig. 1-C-4).
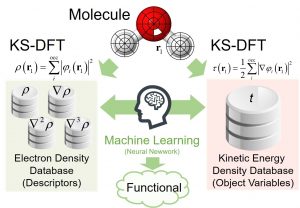
Fig. 1-C-3
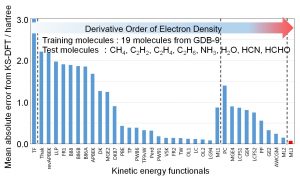
Fig. 1-C-4
The success of ML-KEF confirmed the effectiveness of the Grid-to-Grid type machine learning model. Therefore, a similar approach was examined for correlation energy. For the descriptor, electron density, density gradient, kinetic energy density, HF exchange energy density, and electron density of fractional occupation number were used. In Jacob’s Ladder, which Prof. Perdew used to represent the hierarchy of functionals, these descriptors correspond to Runge 1, 2, 3, 4, and 5, respectively. The objective function was CCSD(T)/CBS correlation energy density. Nakai’ Group has proposed a composite method for estimating CCSD(T)/CBS correlation energy from those of MP2/V(D,T,Q) Z, CCSD/V(D,T)Z, CCSD(T)/VDZ. We also proposed a method (Grid-EDA) that divides the energy obtained by quantum chemistry calculation into energy densities for each spatial grid. Using these proprietary techniques, the CCSD(T)/CBS correlated energy density was estimated. A machine learning type electronic correlation (ML-EC) model was constructed from the above descriptors and objective functions using a neural network in a similar same way to ML-KEF. The ML-EC model using the training set of 15 molecules and the test set of 33 molecules was confirmed to reproduce the CCSD(T)/CBS correlation energy very well (Fig. 1-C-5). The computational time of ML-EC model was overwhelmingly shorter than those of the conventional methods such as the extrapolation method and the composite method for estimating the CCSD(T)/CBS correlation energy (Fig. 1-C-6).
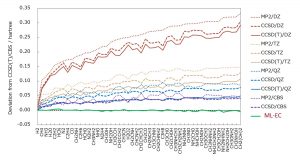
Fig. 1-C-5
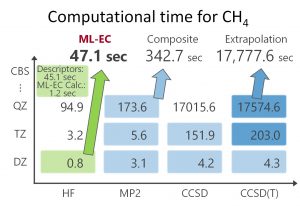
Fig. 1-C-6
Key Literature
<ML-KEF>
- J. Seino, R. Kageyama, M. Fujinami, Y. Ikabata, H. Nakai, “Semi-local machine-learned kinetic energy density functional with third-order gradients of electron density”, J. Chem. Phys., 148, 241705 (2018).
<ML-EC>
- T. Nudejima, Y. Ikabata, J. Seino, T. Yoshikawa, H. Nakai, “Machine-learned electron correlation model based on correlation energy density at complete basis set limit”, J. Chem. Phys., 151, 024104 (2019).
- Y. Ikabata, R. Fujisawa, J. Seino, T. Yoshikawa, H. Nakai, “Machine-learned electron correlation model based on frozen core approximation”, J. Chem. Phys., 153, 184108 (2020).
<Composite>
- J. Seino, H. Nakai, “Informatics-Based Energy Fitting Scheme for Correlation Energy at Complete Basis Set Limit”, J. Comput. Chem., 37, 2304 (2016).
