1-B. Practical two-component relativistic methods
LUT | FCP | PCC
LUT
In order to accurately describe the electronic state of a compound containing all the elements in the periodic table, it is necessary to solve the Dirac equation, which is derived by combining quantum mechanics with special relativity. Since the solution of this Dirac equation includes not only the electronic component but also the positronic component, the computational cost (time, memory) becomes enormous, and the size of the molecule that can be calculated is limited. On the other hand, only the electronic component is important in many cases of chemistry. Therefore, various two-component relativistic methods have been developed that separate the electronic and positronic components by unitary transformation and solve the equation of only the electronic component. Among them, the infinite-order two-component (IOTC) method or the exact two-component (X2C) method can completely separate the electronic and positronic components, and gives the equivalent result as the four-component method that directly solves the Dirac equation. However, the computational cost of the unitary conversion itself for constructing the two-component Hamiltonian is high, and as a result, the computational time may be longer than that of the four-component method (Fig. 1-B-1).

Fig. 1-B-1
Nakai’s Group has developed a local unitary transformation (LUT) method that performs IOTC transformation for each subsystem, focusing on the locality of the relativistic effect. Electronic motions generally approach the speed of light near the inner shell of an atom, and their velocity decreases sharply as they are apart from the nucleus. The LUT method uses this property to limit the range to which the unitary transformation is applied to only the space at a distance below the threshold. As a result, both computational times for the conversion of the one- and two-electron terms become O(N) by the the LUT method, whereas they are O(N3) and O(N5) in the conventional method, respectively,
Namely, linear scaling is achieved. The LUT method for the one-electron term is the equivalent theory as the DLU method proposed by Professor Markus Reiher et al. Note that our LUT method is the only method that improves the efficiency up to the conversion of the two-electron term. As a further efficiency improvement, we also proposed a method of creating a database of LUT-IOTC-transformed two-electron terms for the basis functions of each element.
By combining the LUT method and the DC method, linear scaling is achieved in all steps of the two-component relativistic calculation (Fig. 1-B-2). In fact, this was confirmed by the calculation of the n-mer of HCl molecules (Fig. 1-B-3). Furthermore, it should be noted that the computational time of the two-component relativistic calculation based on the LUT method is close to that of the non-relativistic calculation (Fig. 1-B-3). This means that our LUT and DC methods have made it possible to “break away from the non-relativistic Schrödinger equation and shift to a paradigm of quantum chemistry calculations based on the relativistic Dirac equation,” which has not been possible for many years in the field of quantum chemistry.
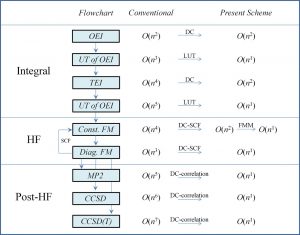
Fig. 1-B-2
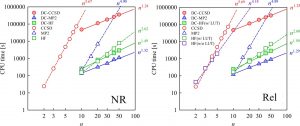
Fig. 1-B-3
Key Literature
<LUT>
- J. Seino, H. Nakai, “Local unitary transformation method for large-scale two-component relativistic calculations: Case for a one-electron Dirac Hamiltonian”, J. Chem. Phys., 136, 244102 (2012).
- J. Seino, H. Nakai, “Local unitary transformation method for large-scale two-component relativistic calculations: Extension to two-electron Coulomb interaction”, J. Chem. Phys., 137, 114101 (2012).
- C. Takashima, J. Seino, H. Nakai, “Database-assisted local unitary transformation method for two-electron integrals in two-component relativistic calculations”, Chem. Phys. Lett., 777, 138691 (2021).
<LUT+DC>
- J. Seino, H. Nakai, “Local unitary transformation method toward practical electron correlation calculations with scalar relativistic effect in large-scale molecules”, J. Chem. Phys., 139, 034109 (2013).
FCP
In heavy atoms where the relativistic effect is particularly important, it is necessary to handle a large number of core electrons in addition to valence electrons. In such cases, a pseudopotential (PP) scheme that replaces the contribution of core electrons with a potential is commonly used. Some PPs use a nodeless potential function in the core region, and others use a nodal potential function. In general, the latter is expected to give a more accurate description. However, since the basis functions of valence electrons are designed to maintain orthogonality with the nodal potential function, unexpected behavior of valence electrons may lead to non-physical results. For example, the case that the two-component relativistic levels when determining the inner-shell potential and the two-component relativistic calculation for valence electrons are significantly different. Nakai’s Group proposed a frozen core potential (FCP) method that theoretically connects valence-electron calculation by PP and all-electron calculation (Fig. 1-B-4).
Furthermore, it has been extended to a method of relaxing the core orbitals (spinors) by the effect of valence electrons. This makes it possible to correctly reproduce core-level chemical shifts due to the molecular environment.
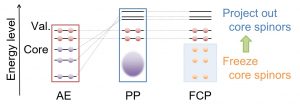
Fig. 1-B-4
Key Literature
<FCP>
- J. Seino, M. Tarumi, H. Nakai, “Frozen core potential scheme with a relativistic electronic Hamiltonian: theoretical connection between the model potential and all-electron treatments”, Chem. Phys. Lett., 592, 341 (2014).
- Y. Nakajima, J. Seino, M. Hayami, H. Nakai, “Relativistic frozen core potential scheme with relaxation of core electrons”, Chem. Phys. Lett., 663, 97 (2016).
PCC
In the two-component relativistic method, the four-component relativistic Hamiltonian is separated into electronic and positronic components by unitary transformation, and the wave function and energy are calculated using only the electronic Hamiltonian. Two-component relativistic methods that give results equivalent to four-component method within the no-pair approximation have been developed: namely, IOTC and X2C. Since the two-component wavefunction includes the effect of (inverse) unitary transformation, the molecular property calculations with the two-component wavefunction give different results from those with the four-component wavefunction.
Such an effect is called a picture change (PC). However, in many quantum chemistry programs, relativistic DFT calculation is performed using the electronic density evaluated by directly using the two-component (or one-component) wavefunction. We have shown that by adopting the unitary-transformed density operator, the electronic density calculated with a two-component (or one-component) wavefunction agree well with that of the four-component wavefunction (Fig. 1-B-5 (left)). Furthermore, we proposed a relativistic DFT calculation method based on this picture change correction (PCC) electron density (Fig. 1-B-5 (right)). We further proposed a local unitary transformation (LUT) of the density operator to improve the calculation efficiency. Furthermore, we proposed a different method using the density matrix obtained by performing the inverse unitary transformation of the two-component wavefunction. We hope that the PCC-type relativistic DFT, which is the correct treatment from the theoretical point of view, will be widely used in the future.
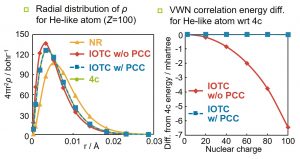
Fig. 1-B-5
Key Literature
<PCC>
- T. Oyama, Y. Ikabata, S. Seino, H. Nakai, “Relativistic density functional theory with picture-change corrected electron density based on infinite-order Douglas-Kroll-Hess method”, Chem. Phys. Lett., 680, 37 (2017).
<LUT-PCC>
- Y. Ikabata, T. Oyama, M. Hayami, J. Seino, H. Nakai, “Extension and acceleration of relativistic density functional theory based on transformed density operator”, J. Chem. Phys., 150, 164104 (2019).
<DM-PCC>
- T. M. Maier, Y. Ikabata, H. Nakai, “Efficient semi-numerical implementation of relativistic exact exchange within the infinite-order two-component method using a modified chain-of-spheres method”, J. Chem. Theory Comput., 15, 4745 (2019).
<Review>
- Y. Ikabata, H. Nakai, “Picture-change correction in relativistic density functional theory”, Phys. Chem. Chem. Phys., 23, 15458 (2021).
