1-A. Practical electron-correlation and excited-state calculation methods

DC

As the range of applications of quantum chemistry calculations expands, the opportunities to adopt more realistic models increase. In such a case, the problem is the relationship between the system size and the computational time. For example, even the commonly used density functional theory (DFT) and Hartree-Fock (HF) calculations require computational times of O(N^3-4) with respect to the system size (N). Various linear scaling methods have been proposed to solve this problem, and the divide-and-conquer (DC) DFT/HF method is one of them. The DC-DFT/HF method makes good use of the property that the Fock and density matrices are relatively localized whereas the molecular orbital is delocalized (Fig. 1-A-1). When defining the subsystem, introducing a buffer region can reduce the error due to the cleavage of the chemical bond. Furthermore, adopting a common Fermi level for all the subsystems allows us to describe a non-integer number of electrons in the subsystem. As a result, it can be applied to various systems including delocalized electron systems, and the density matrix of the entire system and its energy can be obtained simply by specifying the charge/spin multiplicity of the entire system.

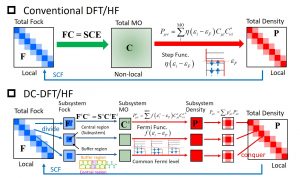
Fig. 1-A-1

The problem between the system size and computational time becomes more serious as the calculational level is more accurate. In the second-order Møller-Plesset perturbation (MP2) method, the coupled cluster with singles and doubles (CCSD) method, and the CCSD (T) method in which perturbative triples are added to CCSD, the computational times increase as O(N⁵), O(N⁶), and O(N⁷), respectively (Fig. 1-A-2). Nakai’s Group has extended the DC method to various electron-correlation methods and excited-state calculation methods, and confirmed their usefulness.

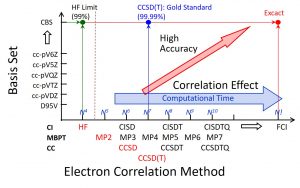
Fig. 1-A-2

In the DC-correlation method, electron correlation calculations such as the MP2, CCSD, and CCSD (T) methods are performed using the molecular orbital and orbital energies of the subsystem obtained by the DC-HF method. However, the subsystem in the DC-HF method involves a buffer region that belongs to multiple subsystems. Therefore, if the correlation energies of the subsystems are simply summed up, the problem of double counting arises. This theoretical problem was solved by adopting the energy density analysis (EDA) proposed by Nakai (Fig. 1-A-3).

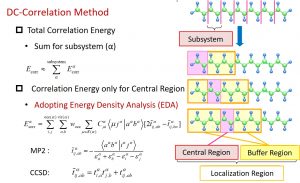
Fig. 1-A-3

When the DC-correlation method is used, the computational times for MP2, CCSD, and CCSD (T) calculations become linear with respect to the system size. In fact, numerical calculations for polyene systems showed that the computational time of DC-CCSD(T) calculation becomes linear-scaling and was reduced from (estimated) 10,000 days in the conventional method to one day (Fig. 1-A-4).

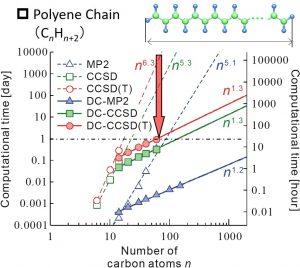
Fig. 1-A-4

The DC-excited-state method performes excitation-state calculations such as the TDDFT and SACCI methods for the excitation center using the molecular orbital and orbital energy of the subsystem obtained by the DC-HF method. Therefore, the actual computational time corresponds to the excited state calculation of the subsystem. Therefore, the computational time is approximately constant, that is, O(N⁰), no matter how large the whole system becomes.

Photoactive yellow protein (PYP) is a water-soluble protein found in purple sulfur bacteria and controls negative phototaxis. Although the excitation center of this photoreceptive protein is p-coumaric acid, a long wavelength shift (red shift) occurs in the protein compared to the solution state. The DC-TDDFT and DC-SACCI methods made it possible to calculate the excited state of the entire PYP system, and the long wavelength shift of excitation energy could be described correctly for the first time (Fig. 1-A-5).

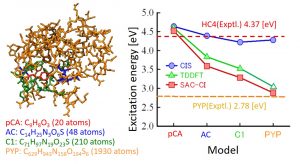
Fig. 1-A-5

The DC-excited-state method cannot deal with the charge transfer excited state beyond the subsystem and the excited state involving delocalized orbitals. This is a common issue to all other fragment-type excited-state calculation methods. Nakai’s Group was the first in the world to solve this issue by focusing on the fact that the pole of the dynamic polarizability contains information on the excited state. Three formulas exist for calculating dynamic polarizability that give equivalent results: coupled perturbation self-consistent field (CPSCF), random phase approximation (RPA), and Green’s function (GF) (Fig. 1-A-6).

Fig. 1-A-6

Computations for many frequencies are required to identify the poles of dynamic polarizability. Taking this into account, the DC-GF type excited-state method is clarified to be the shortest computational time (Fig. 1-A-7). The DC-GF-CCLR method was developed by formulating the GF expression for the linear-response coupled-cluster (CCLR) method as in the case of the HF/DFT level.

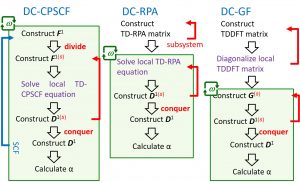
Fig. 1-A-7

Trioxotriangulene (TOT) is a stable organic radical molecule synthesized by Professor Yasushi Morita’s group (Aichi Institute of Technology). TOT π-stacked materials demostrate various attractive functions: for example, the absorption of the near-infrared light with a wavelength of 1000 nm or more. Since HOMOs and LUMOs of TOT π-stacked materials are delocalized throughout the whole systems, the standard fragment-type excited-state calculation methods cannot be applied. By adopting the DC-GF type excited-state calculation method, we could demonstrate the near-infrared light absorption for TOT π-stacked materials of 30-mer or more (Fig. 1-A-8).

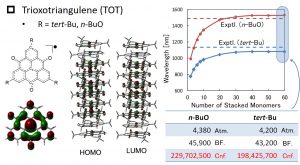
Fig. 1-A-8

Key Literature

＜DC-DFT/HF Method＞

T. Akama, M. Kobayashi, H. Nakai, “Implementation of divide-and-conquer method including Hartree-Fock exchange interaction”, J. Comput. Chem., 28, 2003 (2007).

＜DC-Correlation Method＞

M. Kobayashi, Y. Imamura, H. Nakai, “Alternative Linear-Scaling Methodology for the Second-Order Møller-Plesset Perturbation Calculation Based on the Divide-and-Conquer Method”, J. Chem. Phys., 127, 074103 (2007).
M. Kobayashi, H. Nakai, “Extension of linear-scaling divide-and-conquer-based correlation method to coupled cluster theory with singles and doubles excitations”, J. Chem. Phys., 129, 044103 (2008).
M. Kobayashi, H. Nakai, “Divide-and-conquer-based linear-scaling approach for traditional and renormalized coupled cluster methods with single, double, and noniterative triple excitations”, J. Chem. Phys., 131, 114108 (2009).

＜DC-type Frequency Dependent Polarizability Calculation＞

T. Touma, M. Kobayashi, H. Nakai, “Time-dependent Hartree-Fock frequency-dependent polarizability calculation applied to divide-and-conquer electronic structure method”, Chem. Phys. Lett., 485, 247 (2010).
H. Nakai and T. Yoshikawa, “Development of an excited-state calculation method for large systems using dynamical polarizability: A divide-and-conquer approach at the time-dependent density functional level”, J. Chem. Phys., 146, 124123 (2017).

＜DC-Excited-State Method＞

T. Yoshikawa, M. Kobayashi, A. Fujii, H. Nakai, “Novel approach to excited-state calculations of large molecules based on divide-and-conquer method: Application to photoactive yellow protein”, J. Phys. Chem. B, 117, 5565 (2013).
H. Nakai and T. Yoshikawa, “Development of an excited-state calculation method for large systems using dynamical polarizability: A divide-and-conquer approach at the time-dependent density functional level”, J. Chem. Phys., 146, 124123 (2017).
T. Yoshikawa, J. Yoshihara, H. Nakai, “Large-scale excited-state calculation using dynamical polarizability evaluated by divide-and-conquer based coupled cluster linear response method”, J. Chem. Phys., 152, 024102 (2020).

＜Dc-Excited-State Calculation of TOT＞

Y. Ikabata, Q. Wang, T. Yoshikawa, A. Ueda, T. Murata, K. Kariyazono, M. Moriguchi, H. Okamoto, Y. Morita, H. Nakai, “Near-infrared absorption of π-stacking columns composed of trioxotriangulene neutral radicals”, npj Quantum Mater., 2, 27 (2017).

＜Review＞

M. Kobayashi, H. Nakai, “Divide-and-conquer approaches to quantum chemistry: Theory and implementation”, pp. 97-127 in ‘Linear-Scaling Techniques in Computational Chemistry and Physics: Methods and Applications’, R. Zalesny, M. G. Papadopoulos, P. Mezey, J. Leszczynski (Eds.) (Springer, 2011).
T. Yoshikawa, H. Nakai, “A linear-scaling divide-and-conquer quantum chemical method for open-shell systems and excited states”, pp. 299-323 in ‘Fragmentation: Toward Accurate Calculations on Complex Molecular Systems’, M. Gordon (Eds.) (Wiley, 2017).

＜Review (in Japanese)＞

H. Nakai, T. Akama, M. Kobayashi, “分割統治法に基づく線形スケーリング法の開発”, Bull. Soc. Discrete Variational Xα, 21, 47 (2008).

Press Release

プレスリリース　早稲田大学「有機分子集合体による近赤外光吸収を実現太陽電池やセンサー、医療分野における検査技術の開発への貢献に期待」
プレスリリース　愛知工業大学「近赤外光を吸収する有機化合物の合成に成功 — 愛知工業大学応用化学科　森田教授・村田准教授の研究グループ」
記事掲載　化学工業日報「早大　愛工大　有機分子ＴＯＴ　近赤外光　強く吸収　センサーなど応用へ」（2017年6月12日朝刊 1面 2段）
記事掲載　日経産業新聞「太陽電池、効率化に道、有機分子、近赤外光も吸収、愛工大など」（2017年7月17日 6面）
記事掲載　OPTRONICS ONLINE「早大ら，有機分子集合体で近赤外光を吸収」（2017年6月9日）
化学ポータルサイトChem-Station掲載　スポットライトリサーチ「近赤外光を吸収する有機分子集合体の発見」（2017年8月10日）